Series Contest luyện thi
Bộ ba số
Nộp bàiPoint: 5
Cho mảng ~A~ gồm ~N~ số nguyên dương đôi một khác nhau ~A_i (1 ≤ i ≤ N)~, và một số nguyên ~S~. Bộ ba được định nghĩa là ~3~ số phân biệt từ ~N~ số đã cho.
Yêu cầu: Hãy chọn bộ ba có tổng lớn nhất và không vượt quá ~S~.
Input
Dòng đầu ghi số nguyên dương ~N, S (N≤10000,S≤ 500000)~.
Dòng tiếp theo là ~N~ số nguyên dương ~(1≤ a[i] ≤ 500000)~.
Output
Một số nguyên duy nhất là tổng lớn nhất cần tìm. Test luôn đảm bảo có kết quả.
Sample Input
6 20
7 9 6 2 1 5
Sample Output
20
Giải thích: Bộ ba có tổng lớn nhất là ~9, 6, 5~. Ta có: ~9+6+5=20 ≤ S~.
Ràng buộc
- Có 30% số test ứng với 30% số điểm có ~N≤100~.
- Có 30% số test ứng với 30% số điểm có ~100≤N≤5000~.
- Có 40% số test ứng với 40% số điểm có ~5000 \le N \le 10000~
Xâu có trọng số lớn nhất
Nộp bàiPoint: 5
Trọng số của một xâu ~S~ là trung bình cộng của các kí tự số trong xâu ~S~ đó. Nếu xâu ~S~ không có chữ số nào thì trọng số là ~0~. Ví dụ xâu ~ab011c2~ có trọng số là ~1~.
Yêu cầu: Cho ~N~ xâu kí tự, hãy tìm xâu có trọng số lớn nhất. Nếu có nhiều xâu có trọng số bằng nhau thì ghi ra xâu đầu tiên tìm được, nếu không tìm thấy xâu có trọng số lớn nhất thì ghi ~0~.
Input
Vào từ file TRONGSO.INP gồm:
- Dòng đầu ghi số nguyên ~N~ là số lượng xâu ~(1 ≤ N ≤ 100)~.
- ~N~ dòng tiếp theo nhập xâu ~S~ có độ dài không quá ~1000~.
Output
Ghi ra file TRONGSO.OUT một xâu là kết quả cần tìm.
Sample Input
3
aaaaaaa
10a3bb2021
100256
Sample Output
100256
Giải thích: ~1 + 0 + 0 + 2 + 5 + 6 = 14;~
~14 / 6 = 2.33~ lớn nhất.
Giới hạn:
- 60% số test có độ dài xâu ~S~ không quá ~255~ ký tự.
- 40% số test có độ dài xâu ~S~ không quá ~1000~ ký tự.
Ước chung nhỏ nhất
Nộp bàiPoint: 5
Ước số chung của dãy số nguyên dương là các số nguyên dương mà tất cả các số trong dãy đều chia hết cho nó. Hôm nay, Tuấn đang học về ước số chung và Tuấn được thầy giáo cho bài toán: Cho một dãy số ~𝐴~ gồm ~N~ số nguyên dương, hãy tìm ước số chung nhỏ nhất khác ~1~. Nói cách khác, Tuấn cần tìm số ~𝐷~ nhỏ nhất, sao cho ~D > 1~ và các số trong dãy số ~𝐴~ đều chia hết cho số ~𝐷~ này.
Yêu cầu: Cho một số ~𝐴~ gồm ~𝑁~ số nguyên dương, hãy giúp Tuấn đưa ra số là ước số chung nhỏ nhất khác ~1~.
Input
Vào từ file UCNN.INP gồm:
- Dòng đầu tiên chứa số nguyên dương ~𝑁~ ~(𝑁 ≤ 10^5)~.
- Dòng tiếp theo gồm ~𝑁~ số nguyên dương ~𝐴_𝑖~ là các phần tử của dãy ~𝐴~ ~(𝐴_𝑖≤10^6)~.
Output
Ghi ra file UCNN.OUT một số nguyên dương ước chung nhỏ nhất của dãy số. Nếu không tồn tại số nguyên dương nào, in ra ~-1~.
Sample Input 1
3
1 2 3
Sample Output 1
-1
Sample Input 2
3
2 4 6
Sample Output 2
2
Giới hạn:
- Subtask 1 (60% số điểm): ~𝑁≤10^3, 𝐴_𝑖≤10^5~.
- Subtask 2 (40% số điểm): Không có ràng buộc gì thêm
Đoạn con
Nộp bàiPoint: 5
Cho dãy số nguyên ~A~ gồm ~N~ phần tử ~A_1, A_2, ..., A_N~ hãy tìm:
- Dãy con (không cần phải liên tiếp) khác rỗng có tổng lớn nhất.
- Đoạn con liên tiếp khác rỗng có tổng lớn nhất.
Input
Vào từ file DOANCON.INP gồm:
- Dòng đầu tiên là số lượng test ~T (1 ≤ T ≤ 10)~.
- Mỗi bộ test gồm ~2~ dòng:
- Dòng đầu tiên gồm số ~N (1 ≤ N ≤ 10^5)~.
- Dòng tiếp theo ~N~ số nguyên ~A_1, A_2, ..., A_N (-10^4 ≤ A_i ≤ 10^4)~.
Output
Ghi ra file DOANCON.OUT gồm:
- Với mỗi bộ test ghi ra trên một dòng hai số là hai tổng lớn nhất theo thứ tự yêu cầu.
Sample Input
2
4
1 2 3 4
6
2 -1 2 3 4 -5
Sample Output
10 10
11 10
Giới hạn:
- Subtask 1 (50% số điểm): ~N ≤ 20~
- Subtask 2 (50% số điểm): Không có ràng buộc gì thêm
Giá trị nhỏ nhất
Nộp bàiPoint: 5
Cho dãy số gồm N phần tử a1, a2, .., aN. Hãy tìm hai chỉ số i và j sao cho |ai - aj| nhỏ nhất với (i < j).
Input
Từ file ABSMIN.INP gồm:
- Dòng 1: Một số nguyên dương ~N (2 ≤ N ≤ 2*10^5)~.
- Dòng 2: ~N~ số nguyên ~a_1, a_2, .., a_N (|a_i| ≤ 10^9)~.
Output
Ghi ra file GTNN.OUT một số nguyên duy nhất là giá trị ~|a_i - a_j|~ nhỏ nhất tìm được.
Sample Input
6
-4 3 -9 0 10 5
Sample Output
2
Ràng buộc:
- 30% số test ứng với 30% số điểm có ~N ≤ 2000~.
Cặp số chia hết cho 3
Nộp bàiPoint: 5
Cho dãy ~a~ gồm ~n~ số nguyên dương. Hãy cho biết có bao nhiêu cặp số trong dãy có tổng chia hết cho ~3~. Nói cách khác, bạn phải đếm xem có bao nhiêu cặp chỉ số ~i, j (1 ≤ i < j ≤ n)~ sao cho tổng ~a_i + a_j~ chia hết cho ~3~.
Input
Dữ liệu vào: Từ file DIV3.INP gồm:
- Dòng 1: Một số nguyên duy nhất ~n (1 ≤ n ≤ 10^5 )~.
- Dòng 2: ~n~ số nguyên dương ~a_1, a_2, ..., a_n~ ~(1 ≤ a_i ≤ 10^5 , ∀i=1→n)~ là các phần tử của dãy.
Output
Ghi ra file DIV3.INP gồm một số là số lượng cặp số của dãy a có tổng chia hết cho ~3~.
Sample Input 1
5
3 4 2 3 4
Sample Output 1
3
Giải thích: ~3~ cặp số tìm được có chỉ số là: ~(1,4) (2,3) (3,5)~.
Sample Input 2
4
3 6 9 12
Sample Output 2
6
Giải thích: ~6~ cặp số tìm được có chỉ số là: ~(1,2) (1,3), (1,4), (2,3) (2,4) (3,4)~.
Ràng buộc:
- Subtask 1 (50% số điểm): có ~1≤ n ≤10^3~.
- Subtask 2 (50% số điểm): Không có ràng buộc gì thêm.
Xâu nhị phân
Nộp bàiPoint: 5
Cho ~T~ xâu ~S~. Mỗi xâu chỉ chứa kí tự ~0~ hoặc ~1~. Một xâu gọi là xâu đẹp khi xâu chứa ít nhất một kí tự ~1~ và các kí tự ~1~ phải đứng cạnh nhau. Bạn có thể sử dụng phép xóa kí tự ~0~.
Yêu cầu: Hãy cho biết với mỗi xâu cần ít nhất bao nhiêu phép xóa để trở thành xâu đẹp (mỗi phép xóa chỉ được xóa ~1~ kí tự). Nếu xâu không thể trở thành xâu đẹp thì xuất ~-1~.
Input
Vào từ file BISTR.INP gồm
- Dòng thứ nhất chứa số ~T (1 ≤ T ≤ 1000)~ - Thể hiện số lượng bộ test
- ~T~ dòng tiếp theo mỗi dòng chứa ~1~ xâu ~S~ ~(1 ≤ |S| ≤ 100,~ với ~|S|~ là độ dài xâu ~)~.
Output
Ghi ra file BISTR.OUT gồm ~T~ dòng, ứng với mỗi dòng là kết quả cần tìm.
Sample Input
3
010011
0
1111000
Sample Output
2
-1
0
Ràng buộc:
- Subtask 1 (50% số test): ~1 ≤ T ≤ 50~ và ~1 ≤ |S| ≤ 10~.
- Subtask 2 (50% số test): Không có ràng buộc gì thêm.
Phương trình
Nộp bàiPoint: 5
Cho tập ~n~ số nguyên dương ~W = {w_1, w_2, w_3, ..., w_n}~.
Yêu cầu: Hãy đếm số phương trình bậc hai ~ax^2 + bx + c = 0~ khác nhau tạo được thỏa mãn điều kiện:
- Ba số ~a,b,c~ được lấy từ tập ~W = {w_1, w_2, w_3, ..., w_n}~.
- Ba số ~a,b,c~ đôi một khác nhau.
- Phương trình có ~1~ nghiệm ~x = -1~.
Sample Input
3
1 2 3
Sample Output
2
Giải Thích: PT có ~2~ tập nghiệm là
- ~a=1, b=3, c=2~
- ~a=2, b=3, c=1~
Ràng buộc:
- Subtask 1: ~n ≤ 300; w_i ≤ 10^6~;
- Subtask 2: ~n ≤ 3000; w_i ≤ 10^6~;
- Subtask 3: ~n ≤ 3000; w_i ≤ 10^9~;
- Subtask 4: ~n ≤ 300000; w_i = i~;
Chia bi
Nộp bàiPoint: 5
Ba anh em An, Bình, Phúc được mẹ mua cho ba hộp bi có số viên bi tương ứng là ~a, b, c~ (số bi trong mỗi hộp khác nhau). Bình biết anh An sẽ nhường cho mình lấy hộp có số bi nhiều hơn và Bình cũng sẽ nhường em Phúc hộp có số bi nhiều nhất.
Hãy viết chương trình nhập vào ba số nguyên có giá trị đôi một khác nhau tương ứng với số bi trong ba hộp mà mẹ mua, chương trình sẽ trả về số bi mà Bình được nhận. (Số bi trong mỗi hộp không vượt quá ~100~)
Sample Input
5 3 4
Sample Output
4
Đếm số
Nộp bàiPoint: 5
Cho ~3~ số nguyên dương ~x, n, m~. Hãy đếm xem có bao nhiêu số nguyên dương ~y~ thỏa mãn:
- ~y\le n~
- ~x \times y~ chia hết cho ~m~
Yêu cầu: Cho trước ~x, n, m~, hãy lập trình tìm số lượng số ~y~ thỏa mãn.
Input
- Một dòng chứa ~3~ số ~x, n, m ( x, n, m\le 10^{16})~.
Output
- Một số nguyên là số lượng số nguyên ~y~ thỏa mãn yêu cầu của bài toán.
Ràng buộc
- Subtask ~1~ (~50\%~ số điểm): ~n \le 10^8~.
- Subtask ~2~ (~50\%~ số điểm): không có ràng buộc gì thêm.
Sample Input
6 13 8
Sample Output
3
Giải thích:
Có ~3~ giá trị y thỏa mãn là: ~4~; ~8~; ~12~
Cặp số
Nộp bàiPoint: 5
Cho dãy số nguyên ~a_1, a_2,…, a_n~ và số nguyên ~S~. Hãy đếm xem có bao nhiêu cặp chỉ số ~(i,j)~ với ~i≠j~ mà tổng của ~a_i+a_j = S~.
Input
- Dòng thứ nhất ghi số nguyên dương ~n~ ~(n ≤ 10^5)~ và số nguyên ~S~ ~(│S│ ≤ 10^9)~.
- Các dòng tiếp theo lần lượt ghi các số ~a_1, a_2,…, a_n~ ~(│ai│ ≤ 10^9)~.
Output
- Một số nguyên duy nhất là số lượng cặp chỉ số ~(i,j)~ thỏa mãn yêu cầu.
Sample Input
10 7
5 2 5 3 4 3 1 6 4 0
Sample Output
7
Siêu đối xứng
Nộp bàiPoint: 5
Một số nguyên dương được gọi là siêu đối xứng nếu tất cả các chữ số của nó giống nhau. Chẳng hạn số ~777~ hoặc ~4444~ là các số nguyên dương siêu đối xứng.
Nhập từ bàn phím một số nguyên dương ~x~. Hãy tìm và in ra màn hình số nguyên dương ~y~ nhỏ nhất sao cho tổng ~x + y~ là một số nguyên dương siêu đối xứng.
Input
- Gồm 1 dòng duy nhất chứa số nguyên dương ~x~ ~(1 \leq x \leq 10^{16})~.
Ràng buộc
- Subtask ~1~ (~50\%~ số test): ~x \le 10^6~.
- Subtask ~2~ (~30\%~ số test): ~10^6 < x \le 10^9~.
- Subtask ~3~ (~20\%~ số test): ~10^9 \le x \le 10^{16}~.
Sample Input
45
Sample Output
10
Giải thích
~45 + 10 = 55~
Mua bánh
Nộp bàiPoint: 5
Anh Khôi dự định mua bánh để tặng cho các bạn học sinh lớp luyện thi. Khôi nhận thấy là cần mua tối thiểu ~n~ chiếc bánh để tặng cho học sinh. Tại cửa hàng bán bánh, biết đơn giá mỗi chiếc bánh là ~m~ đồng. Nếu mua từ ~k~ chiếc bánh trở lên thì được giảm ~20~%~~ (có thể mua được nhiều hơn ~n~ chiếc bánh mà chi phí ít tiền hơn)
Yêu cầu: Cho biết ~n~ - số bánh anh Khôi cần mua tối thiểu, ~m~ - giá của một chiếc bánh và ~k~ - số lượng bánh được áp giảm giá. Hãy xác định số tiền tối thiểu anh Khôi cần dùng mua bánh để tặng học sinh?
Input
Từ file BANH.INP
- Một dòng duy nhất chứa ba số nguyên ~n, m, k~ ~( 1 ≤ n ≤ 100; 1 ≤ m ≤ 10000; 1 ≤ k ≤ 100)~.
Output
ghi ra file BANH.OUT
- Ghi một số nguyên là kết quả tìm được theo yêu cầu (nếu kết quả không là số nguyên thì chỉ giữ lại phần nguyên).
Sample Input
10 1000 5
Sample Output
8000
Số chính phương lẻ
Nộp bàiPoint: 5
Cho số tự nhiên ~n~. Hãy xác định các số chính phương lẻ trong khoảng từ ~1~ đến ~n~ và tổng của chúng?
Input
từ file CPL.INP:
- Một dòng chứa số ~n~ ~(0 < n < 10^{12})~
Output
ghi ra file CPL.OUT gồm hai dòng:
- Dòng 1: chứa ~1~ số là số lượng các số chính phương lẻ.
- Dòng 2: chứa ~1~ số là tổng của các số chính phương lẻ theo yêu cầu.
Sample Input
9
Sample Output
2
10
Ràng buộc:
- SubTask1 (50% số điểm): ~n ≤ 10^6~
- SubTask1 (50% số điểm): không có ràng buộc gì thêm
Dãy số tăng
Nộp bàiPoint: 5
Dãy số ~a_1, a_2, …, a_n~ được gọi là dãy tăng nếu ~a_1 < a_2, < … < a_n~.
Bạn được cho một dãy số ~b_1, b_2, ..., b_n~ và một số nguyên dương ~d~. Trong mỗi lần thao tác, bạn chọn một phần tử của dãy số và cộng thêm ~d~ vào nó. Số thao tác ít nhất là bao nhiêu để biến đổi dãy số đã cho trở thành dãy số tăng.
Input
- Dòng thứ nhất ghi số nguyên dương ~n~ ~(1 ≤ n ≤ 10^5)~ và số nguyên ~d~ ~(1 ≤ d ≤ 10^9)~.
- Dòng tiếp theo lần lượt ghi các số ~b_1, b_2, ..., b_n~ ~(1 ≤ b_i ≤ 10^9)~.
Output
- Một số nguyên duy nhất là số thao tác ít nhất để biến đổi dãy số đã cho trở thành dãy số tăng.
Ràng buộc:
- SubTask1 (30% số test): ~1 ≤ n, d, b_i ≤ 10^2~
- SubTask2 (30% số test): ~1 ≤ n ≤ 10^3~ và ~1 ≤ d, b_i ≤ 10^6~
- SubTask3 (40% số test): không có thêm ràng buộc nào
Sample Input
4 2
1 3 3 2
Sample Output
3
Giải thích:
- Thao tác ~1~: Cộng thêm ~2~ vào phần tử thứ ba dãy số trở thành ~1, 3, 5, 2;~
- Thao tác ~2~: Cộng thêm ~2~ vào phần tử thứ tư dãy số trở thành ~1, 3, 5, 4;~
- Thao tác ~3~: Cộng thêm ~2~ vào phần tử thứ tư dãy số trở thành ~1, 3, 5, 6~ và là dãy số tăng.
Hình chữ nhật
Nộp bàiPoint: 5
Cho hình chữ nhật gồm ~N~ dòng và ~M~ cột. Các dòng được đánh số từ ~1~ đến ~N~ từ trên xuống dưới. Các cột được đánh số từ ~1~ đến ~M~, từ trái sang phải. Ô ở dòng thứ ~i~, cột thứ ~j~ được gọi là ô ~(i, j)~ và có diện tích là ~1~ đơn vị. Có một số ô đã được điền sẵn kí tự ~'X'~.
Yêu cầu: Tìm hình chữ nhật con có diện tích lớn nhất mà chỉ chứa duy nhất một kí tự ~'X'~.
Input
- Dòng 1: chứa ba số nguyên dương ~N, M, K~ ~(N, M ≤ 500; K ≤ 10^3)~ mô tả kích thước của hình chữ nhật và số lượng kí tự 'X' có trong hình chữ nhật.
- ~K~ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương ~d~ và ~c~ là chỉ số của dòng và cột của ô điền kí tự ~'X'~ ~(d ≤ N, c ≤ M)~.
Output
- Gồm một dòng duy nhất chứa một số là diện tích của hình chữ nhật lớn nhất thỏa mãn yêu cầu của đề bài.
Ràng buộc:
- SubTask1 (50% số test): ~N, M ≤ 50~
- SubTask2 (50% số test): ~N, M ≤ 500~
Sample Input
4 5 4
2 3
2 5
3 1
4 4
Sample Output
9
Giải thích:
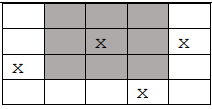
In bảng chữ cái
Nộp bàiPoint: 5
Nhập số nguyên dương N (N<=26). Hãy in bảng chữ cái tiếng anh theo hàng ngang, mỗi hàng có N chữ cái. (Chỉ hàng cuối cùng có thể không đủ N chữ cái).
Input:
Số nguyên dương N
Output:
Bảng chữ cái theo N dòng
Sample Input
10
Sample Output
A B C D E F G H I J
K L M N O P Q R S T
U V W X Y Z


